市場風險管理

根據國際清算銀行(Bank for International Settlements，以下簡稱BIS)於1996年所發布巴塞爾修正案中，明訂將市場風險的計算以VaR風險值作為衡量的指標。

而VaR風險值最大的優點在於，藉由將公司所遭遇的所有風險彙整成一個數值，讓管理階層能夠簡單明瞭地知道公司資產組合所可能面臨之最大損失。因而近十年來，VaR風險值被大量的接納採用來作為管理市場風險的指標工具。

VaR風險值的定義

風險值乃是衡量市場風險的一種方法，其意義為在特定期間及特定機率下，持有單一資產或資產的投資組合，因市場上經濟變數之變動，預期該組合可能產生的最大損失。Hull與White(1998)提出對風險值的定義為：「有100(1. α)%的信心在未來N天內的最大損失不會超過V元」，其中V即為風險值。例如，某一部位在99%信賴水準下之每日風險值為100萬元，亦即平均在100個交易日中，該部位只有1日之損失會超過100萬元。

VaR風險值估算方法

在計算VaR風險值之前，首先需要產生投資組合價值在某段曝險期間之未來分配，或是投資組合價值變動之分配。目前衡量VaR風險值之方式有三種：

• 變異數-共變異數法(Variance-Covariance Approach)
• 歷史模擬法(Historical Simulation Approach)
• 蒙地卡羅模擬法(Monte Carlo Simulation Approach)

(1)變異數-共變異數法(Variance-Covariance Approach)  

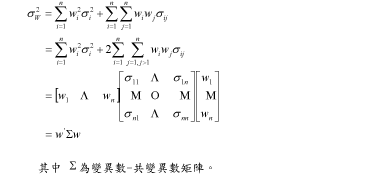
在所有計算風險值的方法中，變異數-共變異數法是最常的計算方式。基本原是假設資產報酬為常態分配及線性，而常態分配的線性組合仍為常態分配。常態分配的個別平均和標準差可以由歷史資料中求得，進而計算投資組合的變異數-共變異數法矩陣，以及在特定機率下的一段期間中所可能產生的最大損失。

股票投資組合VaR 風險值之計算

步驟一：計算股價報酬 

採用連續型報酬，單一股價報酬率計算方式如下：

步驟二：計算股票投資組合之變異數 

若股票投資組合包含n種股票，則投資組合之變異數求算公式為： 

步驟三：股票投資組合 VaR 風險值計算  

VaR 風險值

 其中x為各資產價值

 Marginal VaR

Component VaR  

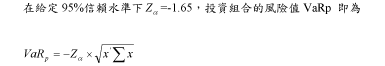
Component VaR是將投資組合的風險分解至各資產，求得各資產的風險值。

Component VaR= Marginal VaR*x

(2)歷史模擬法(Historical Simulation Approach)  

此法由實際之歷史資料求算資產組合風險值，利用持有的資產組合過去一段時間歷史價格之時間序列，配合目前持有資產部位，重新建構資產組合未來報酬分配後，由小而大排序，以百分位數的概念求得在特定信賴水準下之風險值。

歷史模擬法假設未來資產報酬的走勢與過去之報酬趨勢大致相同，並無結構性的變化產生，故只要歷史資料筆數夠多，就能模擬出與過去報酬走勢大致相同的分配。

以下為歷史模擬法估算未來一天風險值的程序步驟：

步驟一：  

以持有之投資組合資產之過去歷史價格，計算某期間內資產之損益報酬率，作為未來相同期間內報酬走勢的基礎，亦即以目前資產之報酬，加上求算出的過去資產之損益報酬率，模擬出資產在未來某段期間內之報酬走勢。

以單一股票模擬為例：

由欲計算風險值當日往前推101天，共可取得101筆之歷史股票價格時間序列：  

求算出100筆的損益報酬率

以這100筆股價損益報酬做為未來報酬的可能變動，再加上目前的股票報酬 R，則可模擬出100筆該股票之未來可能報酬  

依上述步驟，n種股票之模擬報酬皆可同理求出。  

步驟二：  

模擬投資組合未來之報酬，利用步驟一求得n種股票之模擬報酬，而每筆股票的權重為持有部位市價占總部位市價之比率，則投資組合之模擬報酬即為n種股票的模擬報酬之加權平均。

步驟三： 

將投資組合之可能報酬由小至大排序，用以描繪該投資組合的損益分配，然後依據假設的分位數估算不同信賴水準下的風險值。以100筆損益資料為例，若信賴水準為95%，則第5筆資料(100*5%)即為估算之風險值。

(3)蒙地卡羅模擬(Monte Carlo Simulation Approach)

蒙地卡羅模擬法假設資產價格變化行徑符合特定的隨機過程，最常見的像是股價服從幾何布朗運動(Geometric Brownian Motion)，利用隨機的過程，經由模擬方式重覆得到不同情境下的資產損益分配，由於產生次數夠多，模擬之投資組合報酬分配，將會接近真實分配，最後在依據分位數求算相對應之信賴水準下的風險值。

蒙地卡羅模擬法適用於估算線性及非線性商品之風險值，在蒙地卡羅模擬法下每個市場皆有明確的機率分配，因而在模擬的方式下可方便進行敏感性分析及壓力測試。蒙地卡羅模擬法的缺點為所有的交易工具均需訂價模型，計算上相對複雜且模擬的價格與現實價格間仍存有差異。

蒙地卡羅模擬法進行程序如下：  

步驟一：  

建立價格走勢之隨機過程，同時需要估計它們的參數(平均數、波動度與相關係數等)，例如股價評估之幾何布朗運動，它可以下列隨機過程表示：

步驟二：  

隨機從標準常態分配中抽取ε，再給定起始值 S 後，產生下一期股價，如此一直循環產生一條股價路徑，接著求算出股價報酬率。

步驟三：  

模擬所有投資組合中之股價報酬，做法同步驟一、二，只需更改隨機過程之參數(本例之參數為μ與σ)，求得之股價報酬以持有部位市價占總部位市價之比率為權重，加權平均之結果即為該投資組合之模擬報酬。  

步驟四：  

重複步驟三之過程N次(如：1000次)，則可產生風險期間內投資組合報酬之分配。此一步驟與歷史模擬法相同，只是蒙地卡羅模擬法之模擬次數遠高於歷史模擬法。因此，95%信賴水準下之風險值，則為此分配之第5百分位數。  

風險值衡量方法分析